▼ 怎么设计程序,第二版
• Prologue:   How to Program
On this page:
Arithmetic and Arithmetic
Inputs and Output
Many Ways to Compute
One Program, Many Definitions
One More Definition
You Are a Programmer Now
Not!
6.11.0.4
    ← prev  up  next → 

序言: 怎么编程

当你是一个小孩子时，你爸妈教你用手指头数数，Consider a quick look at On Teaching Part I. 然后做一些简单的计算:“1加1等于2”；“1加2等于3”,等等。然后他们将会问你“2加3”等于多少？你将会数一只手的全部手指头。 他们编程，你计算。在某种意义上，那就是编程和计算的全部。

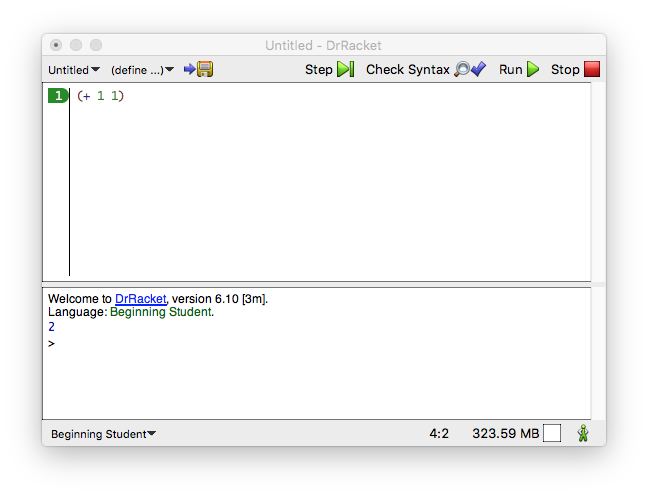
Download DrRacket from its web site.

现在是切换角色的时候了。启动DrRacket。这样会产生如图3的窗口。从“语言菜单”选择“选择语言” ,这打开了一个用于“怎么设计程序”的教学语言的对话框列表。选择“初学者”（初学者语言，或者BSL）然后 点击确定来设置DrRacket。 这些任务完成后，你可以编程了。从最简单的计算开始。你输入

(+ 1 1)

到DrRacket顶部，点击运行，然后2就会显示在底部。

图 3: 认识DrRacket

以上展示了编程是多么简单。你像问小孩子问题一样问DrRacket，然后DrRacket给你计算。 你也可以一次让DrRacket处理几个请求:
(+ 2 2)
(* 3 3)
(- 4 2)
(/ 6 2)
点击运行后,你在DrRacket的底部，看到 4 9 2 3 ，这正是期望的结果。

让我们慢下来一会儿，介绍一些词语:

  • DrRacket的顶部叫做定义区。 在这个区域，你创建程序，叫编辑。只要你在定义区添加一个字或者或者修改一些内容，保存 按钮出现在左上角。当你首次点击保存时， DrRacket会询问你文件的名字，以便它能保存好你的程序。一旦定义区和一个文件关联了，点击保存确保定义区的内容安全地存储在文件里。

  • 程序 包括 一系列的表达式。你已经看到了数学中的表达式。目前，一个表达式是一个普通数字或者 是开始于一个左括号“(”，并且结束于匹配的右括号“)”的内容—DrRacket提倡 屏蔽括号对之间的区域。

  • 当你点击运行, DrRacket对定义区内的表达式求值，在交互区 显示结果。然后,DrRacket,你的忠实的保姆，在提示符处 (>),等着你的命令。 提示符的出现表示DrRacket正等着你输入其他的表达式，然后它就对这些表达式求值，就像定义区的那样:
    > (+ 1 1)

    2

    咋提示符处，输入一个表达式，在你的键盘上点击“返回”或者 or “回车”键 ,然后观察DrRacket响应的结果。喜欢的话，你可以经常这样做:
    > (+ 2 2)

    4

    > (* 3 3)

    9

    > (- 4 2)

    2

    > (/ 6 2)

    3

    > (sqr 3)

    9

    > (expt 2 3)

    8

    > (sin 0)

    0

    > (cos pi)

    #i-1.0

仔细看最后一个数字。它的“#i”前缀是“我真的不知道目前的确切数字”或者是不精确的数字的简称。 不像你的计算器或者其他的编程系统，DrRacket是诚实的。当它不知道准确的数字时，它以特殊的前缀警告你。 后续，我们将会向你展示一些关于“计算数字”的奇怪的事实。你会真正意识到，DrRacket会发出这样的警告。

到现在为止，你也许会想DrRacket能否一次相加多于2个数字，是的，它可以！ 事实上，它能使用两种不同的方式实现它:
> (+ 2 (+ 3 4))

9

> (+ 2 3 4)

9

第一个是嵌套算法，就像你从学校知道的一样。 第二是BSL 算法;而后者是自然的，因为在这种情形中，你总是使用括号来把操作符和数字组合在一起。

在 BSL中,This book does not teach you Racket, even if the editor is called DrRacket. See the Preface, especially the section on DrRacket and the Teaching Languages for details on the choice to develop our own language. 每次你想使用一个“计算操作”，你写下一个开放的括号，你希望执行的操作，比如说+,数字在这个操作上要可以运行（以空格或者甚至换行符）最后，一个闭合的括号。操作后面跟的项是操作数。 嵌套算法意味着你可以使用表达式作为操作数，这也是为什么
> (+ 2 (+ 3 4))

9

是一个语法正确的程序。你喜欢的话，你可以经常这样做:
> (+ 2 (+ (* 3 3) 4))

15

> (+ 2 (+ (* 3 (/ 12 4)) 4))

15

> (+ (* 5 5) (+ (* 3 (/ 12 4)) 4))

38

除了你的耐心之外，嵌套没有限制。

通常，当DrRacket替你计算时，他使用你熟悉和喜欢的数学规则，像你一样，只有当所有的操作数是普通数字时，它才能决定一个加法的结果。 如果一个操作数是一个带括号的操作符表达式—以一个“(”和一个操作符开始—它先确定嵌套表达式的结果。 和你不一样，它从来不需要仔细思考需要先计算哪一个表达式— 因为这个第一条规则，是存在的唯一的规则。

DrRacket的便利之处是括号是有意义的。你必须输入全部的括号，你也许不会输入太多。 例如，尽管你的数学老师可以接受额外的括号，但是BSL并非如此。 这个表达式(+ (1) (2))包含太多括号了，DrRacket会让你毫不含糊的知道:
> (+ (1) (2))

function call:expected a function after the open parenthesis, found a number

一旦你习惯了BSL编程，你会看到它并不总是值得的。首先，你可以一次在几个操作数上使用几个操作符， 如果这样做是自然的：
> (+ 1 2 3 4 5 6 7 8 9 0)

45

> (* 1 2 3 4 5 6 7 8 9 0)

0

如果你不知道一个操作符，作用在几个操作数的结果是什么，输入一个示例到交互区，点击“回车”; DrRacket让你知道它是否以及怎么运行的。或者使用HelpDesk阅读文档。 As you may have noticed, the names of operations in the on-line text are linked to the documentation in HelpDesk. 第二，当你读其他人写的程序时，你将要不得不仔细思考哪一个表达式需要首先进行计算。括号和嵌套结构将会立即告诉你。

在这部分内容中，编程就是写可理解的算术表达式，计算就是确定它们的值。 借助DrRacket，可以轻松探索这类编程和计算。

算法还是算法

如果编程仅仅是数字和算术，它将会像数学一样令人烦恼。幸运的是，比数字更多的东西可以编程：文本，定理，图像，还有更多。 Just kidding: mathematics is a fascinating subject, but you won’t need much of it for now.

在BSL中，你需要知道的第一件事是，文本是任何一个键盘输入的以双引号(") 包含的字符序列。 我们叫它字符串。这样子, "hello world" 是一个相当好的字符串； 当DrRacket对这个字符串求值时，它只是在交互区回显它。 when DrRacket evaluates this string, it 像一个数字那样:
> "hello world"

"hello world"

的确，许多人的第一个程序，就是准确的显示这个字符串。

此外，你需要知道除了数字算术之外，DrRacket也知道字符算术。 所以，这里有两次交互来说明这种算术形式：
> (string-append "hello" "world")

"helloworld"

> (string-append "hello " "world")

"hello world"

就像+, string-append是一个操作;它通过添加第二个字符串到第一个字符串的末尾，产生了一个字符串。 像第一次交互所示，它仅仅在字面上操作,没有在这两个字符串之间，添加任何内容：没有空格，没有逗号，什么都没有。 这样子，如果你想看到这个短语"hello world"，你真的需要在这些单词中的其中一个的某处添加一个空格；如第二个交互所示。当然，使用这两个单词创建这个短语，最自然的方式是输入

(string-append "hello" " " "world")

因为 string-append, 像 +一样, 能够根据需要，处理任意多的操作数。

你可以用字符串做更多的事情，而不仅仅是追加它们。 You can do more with strings than append them. You can extract pieces from a string, reverse them, render all letters uppercase (or lowercase), strip blank spaces from the left and right, and so on. And best of all, you don’t have to memorize any of that. If you need to know what you can do with strings, look up the term in HelpDesk.Use F1 or the drop-down menu on the right to open HelpDesk. Look at the manuals for BSL and its section on pre-defined operations, especially those for strings.

If you looked up the primitive operations of BSL, you saw that primitive (sometimes called pre-defined or built-in) operations can consume strings and produce numbers:
> (+ (string-length "hello world") 20)

31

> (number->string 42)

"42"

There is also an operation that converts strings into numbers:
> (string->number "42")

42

If you expected “forty-two” or something clever along those lines, sorry, that’s really not what you want from a string calculator.

The last expression raises a question, though. What if someone uses string->number with a string that is not a number wrapped within string quotes? In that case, the operation produces a different kind of result:
> (string->number "hello world")

#false

This is neither a number nor a string; it is a Boolean. Unlike numbers and strings, Boolean values come in only two varieties: #true and #false. The first is truth, the second falsehood. Even so, DrRacket has several operations for combining Boolean values:
> (and #true #true)

#true

> (and #true #false)

#false

> (or #true #false)

#true

> (or #false #false)

#false

> (not #false)

#true

and you get the results that the name of the operation suggests. (Don’t know what and, or, and not compute? Easy: (and x y) is true if x and y are true; (or x y) is true if either x or y or both are true; and (not x) results in #true precisely when x is #false.)

It is also useful to “convert” two numbers into a Boolean:
> (> 10 9)

#true

> (< -1 0)

#true

> (= 42 9)

#false

Stop! Try the following three expressions: (>= 10 10), (<= -1 0), and (string=? "design" "tinker"). This last one is different again; but don’t worry, you can do it.

With all these new kinds of data— yes, numbers, strings, and Boolean values are data— and operations floating around, it is easy to forget some basics, like nested arithmetic:
(and (or (= (string-length "hello world")
            (string->number "11"))
         (string=? "hello world" "good morning"))
     (>= (+ (string-length "hello world") 60) 80))
What is the result of this expression? How did you figure it out? All by yourself? Or did you just type it into DrRacket’s interactions area and hit the “return” key? If you did the latter, do you think you would know how to do this on your own? After all, if you can’t predict what DrRacket does for small expressions, you may not want to trust it when you submit larger tasks than that for evaluation.

Before we show you how to do some “real” programming, let’s discuss one more kind of data to spice things up: images.To insert images such as this rocket into DrRacket, use the Insert menu. Or, copy and paste the image from your browser into DrRacket. When you insert an image into the interactions area and hit “return” like this

>

DrRacket replies with the image. In contrast to many other programming languages, BSL understands images, and it supports an arithmetic of images just as it supports an arithmetic of numbers or strings. In short, your programs can calculate with images, and you can do so in the interactions area. Furthermore, BSL programmers— like the programmers for other programming languages— create libraries that others may find helpful. Using such libraries is just like expanding your vocabularies with new words or your programming vocabulary with new primitives. We dub such libraries teachpacks because they are helpful with teaching.

Add (require 2htdp/image) to the definitions area, or select Add Teachpack from the Language menu and choose image from the Preinstalled HtDP/2e Teachpack menu.

One important library— the 2htdp/image library — supports operations for computing the width and height of an image:

(* (image-width ) (image-height ))

Once you have added the library to your program, clicking RUN gives you 1176 because that’s the area of a 28 by 42 image.

You don’t have to use Google to find images and insert them in your DrRacket programs with the “Insert” menu. You can also instruct DrRacket to create simple images from scratch:
> (circle 10 "solid" "red")

image

> (rectangle 30 20 "outline" "blue")

image

When the result of an expression is an image, DrRacket draws it into the interactions area. But otherwise, a BSL program deals with images as data that is just like numbers. In particular, BSL has operations for combining images in the same way that it has operations for adding numbers or appending strings:
> (overlay (circle 5 "solid" "red")
           (rectangle 20 20 "solid" "blue"))

image

Overlaying these images in the opposite order produces a solid blue square:
> (overlay (rectangle 20 20 "solid" "blue")
           (circle 5 "solid" "red"))

image

Stop and reflect on this last result for a moment.

As you can see, overlay is more like string-append than +, but it does “add” images just like string-append “adds” strings and + adds numbers. Here is another illustration of the idea:
> (image-width (square 10 "solid" "red"))

10

> (image-width
    (overlay (rectangle 20 20 "solid" "blue")
             (circle 5 "solid" "red")))

20

These interactions with DrRacket don’t draw anything at all; they really just measure their width.

Two more operations matter: empty-scene and place-image. The first creates a scene, a special kind of rectangle. The second places an image into such a scene:
(place-image (circle 5 "solid" "green")
             50 80
             (empty-scene 100 100))
and you get this:Not quite. The image comes without a grid. We superimpose the grid on the empty scene so that you can see where exactly the green dot is placed.

image

As you can see from this image, the origin (or (0,0)) is in the upper-left corner. Unlike in mathematics, the y-coordinate is measured downward, not upward. Otherwise, the image shows what you should have expected: a solid green disk at the coordinates (50,80) in a 100 by 100 empty rectangle.

Let’s summarize again. To program is to write down an arithmetic expression, but you’re no longer restricted to boring numbers. In BSL, arithmetic is the arithmetic of numbers, strings, Booleans, and even images. To compute, though, still means to determine the value of an expression— except that this value can be a string, a number, a Boolean, or an image.

And now you’re ready to write programs that make rockets fly.

Inputs and Output

The programs you have written so far are pretty boring. You write down an expression or several expressions; you click RUN; you see some results. If you click RUN again, you see the exact same results. As a matter of fact, you can click RUN as often as you want, and the same results show up. In short, your programs really are like calculations on a pocket calculator, except that DrRacket calculates with all kinds of data, not just numbers.

That’s good news and bad news. It is good because programming and computing ought to be a natural generalization of using a calculator. It is bad because the purpose of programming is to deal with lots of data and to get lots of different results, with more or less the same calculations. (It should also compute these results quickly, at least faster than we can.) That is, you need to learn more still before you know how to program. No need to worry though: with all your knowledge about arithmetic of numbers, strings, Boolean values, and images, you’re almost ready to write a program that creates movies, not just some silly program for displaying “hello world” somewhere. And that’s what we’re going to do next.

Just in case you didn’t know, a movie is a sequence of images that are rapidly displayed in order. If your algebra teachers had known about the “arithmetic of images” that you saw in the preceding section, you could have produced movies in algebra instead of boring number sequences. Well, here is one more such table:

x =

   

1

   

2

   

3

   

4

   

5

   

6

   

7

   

8

   

9

   

10

y =

   

1

   

4

   

9

   

16

   

25

   

36

   

49

   

64

   

81

   

?
Your teachers would now ask you to fill in the blank, that is, replace the “?” mark with a number.

It turns out that making a movie is no more complicated than completing a table of numbers like that. Indeed, it is all about such tables:

x =

   

1

   

2

   

3

   

4

y =

   

image

   

image

   

image

   

image

To be concrete, your teacher should ask you here to draw the fourth image, the fifth, and the 1273rd one because a movie is just a lot of images, some 20 or 30 of them per second. So you need some 1200 to 1800 of them to make one minute’s worth of it.

You may also recall that your teacher not only asked for the fourth or fifth number in some sequence but also for an expression that determines any element of the sequence from a given x. In the numeric example, the teacher wants to see something like this:

image

If you plug in 1, 2, 3, and so on for x, you get 1, 4, 9, and so on for y— just as the table says. For the sequence of images, you could say something like

y = the image that contains a dot x2 pixels below the top.

The key is that these one-liners are not just expressions but functions.

At first glance, functions are like expressions, always with a y on the left, followed by an = sign, and an expression. They aren’t expressions, however. And the notation you often see in school for functions is utterly misleading. In DrRacket, you therefore write functions a bit differently:

(define (y x) (* x x))

The define says “consider y a function,” which, like an expression, computes a value. A function’s value, though, depends on the value of something called the input, which we express with (y x). Since we don’t know what this input is, we use a name to represent the input. Following the mathematical tradition, we use x here to stand in for the unknown input; but pretty soon, we will use all kinds of names.

This second part means you must supply one number— for x— to determine a specific value for y. When you do, DrRacket plugs the value for x into the expression associated with the function. Here the expression is (* x x). Once x is replaced with a value, say 1, DrRacket can compute the result of the expressions, which is also called the output of the function.

Click RUN and watch nothing happen. Nothing shows up in the interactions area. Nothing seems to change anywhere else in DrRacket. It is as if you hadn’t accomplished anything. But you did. You actually defined a function and informed DrRacket about its existence. As a matter of fact, the latter is now ready for you to use the function. Enter

(y 1)

at the prompt in the interactions area and watch a 1 appear in response. The (y 1) is called a function application in DrRacket.Mathematics also calls y(1) a function application, but your teachers forgot to tell you. Try

(y 2)

and see a 4 pop out. Of course, you can also enter all these expressions in the definitions area and click RUN:
(define (y x) (* x x))
 
(y 1)
(y 2)
(y 3)
(y 4)
(y 5)
In response, DrRacket displays: 1 4 9 16 25 , which are the numbers from the table. Now determine the missing entry.

What all this means for you is that functions provide a rather economic way of computing lots of interesting values with a single expression. Indeed, programs are functions; and once you understand functions well, you know almost everything there is to know about programming. Given their importance, let’s recap what we know about functions so far:

  • First,

    (define (FunctionName InputName) BodyExpression)

    is a function definition. You recognize it as such because it starts with the “define” keyword. It essentially consists of three pieces: two names and an expression. The first name is the name of the function; you need it to apply the function as often as you wish. The second name— called a parameter— represents the input of the function, which is unknown until you apply the function. The expression, dubbed body, computes the output of the function for a specific input.

  • Second,

    (FunctionName ArgumentExpression)

    is a function application. The first part tells DrRacket which function you wish to use. The second part is the input to which you want to apply the function. If you were reading a Windows or a Mac manual, it might tell you that this expression “launches” the “application” called FunctionName and that it is going to process ArgumentExpression as the input. Like all expressions, the latter is possibly a plain piece of data or a deeply nested expression.

Functions can input more than numbers, and they can output all kinds of data, too. Our next task is to create a function that simulates the second table— the one with images of a colored dot— just like the first function simulated the numeric table. Since the creation of images from expressions isn’t something you know from high school, let’s start simply. Do you remember empty-scene? We quickly mentioned it at the end of the previous section. When you type it into the interactions area, like that:
> (empty-scene 100 60)

image

DrRacket produces an empty rectangle, also called a scene. You can add images to a scene with place-image:

> (place-image image 50 23 (empty-scene 100 60))

image

Think of the rocket as an object that is like the dot in the above table from your mathematics class. The difference is that a rocket is interesting.

Next, you should make the rocket descend, just like the dot in the above table. From the preceding section, you know how to achieve this effect by increasing the y-coordinate that is supplied to place-image:
> (place-image image 50 20 (empty-scene 100 60))

image

> (place-image image 50 30 (empty-scene 100 60))

image

> (place-image image 50 40 (empty-scene 100 60))

image

All that’s needed now is to produce lots of these scenes easily and to display all of them in rapid order.

(define (picture-of-rocket height)
  (place-image  50 height (empty-scene 100 60)))

Figure 4: Landing a rocket (version 1)

The first goal can be achieved with a function, of course; see figure 4.In BSL, you can use all kinds of characters in names, including “-” and “.”. Yes, this is a function definition. Instead of y, it uses the name picture-of-rocket, a name that immediately tells you what the function outputs: a scene with a rocket. Instead of x, the function definition uses height for the name of its parameter, a name that suggests that it is a number and that it tells the function where to place the rocket. The body expression of the function is exactly like the series of expressions with which we just experimented, except that it uses height in place of a number. And we can easily create all of those images with this one function:
(picture-of-rocket 0)
(picture-of-rocket 10)
(picture-of-rocket 20)
(picture-of-rocket 30)
Try this out in the definitions area or the interactions area; both create the expected scenes.

The second goal requires knowledge about one additional primitive operation from the 2htdp/universe library : animate.Don’t forget to add the 2htdp/universe library to your definitions area. So, click RUN and enter the following expression:

> (animate picture-of-rocket)

Stop and note that the argument expression is a function. Don’t worry for now about using functions as arguments; it works well with animate, but don’t try to define functions like animate at home just yet.

As soon as you hit the “return” key, DrRacket evaluates the expression; but it does not display a result, not even a prompt. It opens another window— a canvas— and starts a clock that ticks 28 times per second. Every time the clock ticks, DrRacket applies picture-of-rocket to the number of ticks passed since this function call. The results of these function calls are displayed in the canvas, and it produces the effect of an animated movie. The simulation runs until you close the window. At that point, animate returns the number of ticks that have passed.

The question is where the images on the window come from. The short explanation is that animate runs its operand on the numbers 0, 1, 2, and so on,Exercise 298 explains how to design animate. and displays the resulting images. The long explanation is this:

  • animate starts a clock and counts the number of ticks;

  • the clock ticks 28 times per second;

  • every time the clock ticks, animate applies the function picture-of-rocket to the current clock tick; and

  • the scene that this application creates is displayed on the canvas.

This means that the rocket first appears at height 0, then 1, then 2, and so on, which explains why the rocket descends from the top of the canvas to the bottom. That is, our three-line program creates some 100 pictures in about 3.5 seconds, and displaying these pictures rapidly creates the effect of a rocket descending to the ground.

So here is what you learned in this section. Functions are useful because they can process lots of data in a short time. You can launch a function by hand on a few select inputs to ensure that it produces the proper outputs. This is called testing a function. Or, DrRacket can launch a function on lots of inputs with the help of some libraries; when you do that, you are running the function. Naturally, DrRacket can launch functions when you press a key on your keyboard or when you manipulate the mouse of your computer. To find out how, keep reading. Whatever triggers a function application isn’t important, but do keep in mind that (simple) programs are functions.

Many Ways to Compute

When you evaluate (animate picture-of-rocket), the rocket eventually disappears into the ground. That’s plain silly. Rockets in old science fiction movies don’t sink into the ground; they gracefully land on their bottoms, and the movie should end right there.

This idea suggests that computations should proceed differently, depending on the situation. In our example, the picture-of-rocket program should work “as is” while the rocket is in flight. When the rocket’s bottom touches the bottom of the canvas, however, it should stop the rocket from descending any farther.

In a sense, the idea shouldn’t be new to you. Even your mathematics teachers define functions that distinguish various situations:

image

This sign function distinguishes three kinds of inputs: those numbers that are larger than 0, those equal to 0, and those smaller than 0. Depending on the input, the result of the function is +1, 0, or -1.

You can define this function in DrRacket without much ado using a conditional expression:
(define (sign x)
  (cond
    [(> x 0) 1]
    [(= x 0) 0]
    [(< x 0) -1]))
After you click RUN, you can interact with sign like any other function:Open a new tab in DrRacket and start with a clean slate.
> (sign 10)

1

> (sign -5)

-1

> (sign 0)

0

This is a good time to explore what the STEP button does. Add (sign -5) to the definitions area and click STEP for the above sign program. When the new window comes up, click the right and left arrows there.

In general, a conditional expression has the shape
(cond
  [ConditionExpression1 ResultExpression1]
  [ConditionExpression2 ResultExpression2]
  ...
  [ConditionExpressionN ResultExpressionN])
That is, a conditional expression consists of as many conditional lines as needed. Each line contains two expressions: the left one is often called condition, and the right one is called result; occasionally we also use question and answer. To evaluate a cond expression, DrRacket evaluates the first condition expression, ConditionExpression1. If this yields #true, DrRacket replaces the cond expression with ResultExpression1, evaluates it, and uses the value as the result of the entire cond expression. If the evaluation of ConditionExpression1 yields #false, DrRacket drops the first line and starts over. In case all condition expressions evaluate to #false, DrRacket signals an error.

(define (picture-of-rocket.v2 height)
  (cond
    [(<= height 60)
     (place-image  50 height
                  (empty-scene 100 60))]
    [(> height 60)
     (place-image  50 60
                  (empty-scene 100 60))]))

Figure 5: Landing a rocket (version 2)

With this knowledge, you can now change the course of the simulation. The goal is to not let the rocket descend below the ground level of a 100-by-60 scene. Since the picture-of-rocket function consumes the height where it should place the rocket in the scene, a simple test comparing the given height to the maximum height appears to suffice.

See figure 5 for the revised function definition. The definition uses the name picture-of-rocket.v2 to distinguish the two versions. Using distinct names also allows us to use both functions in the interactions area and to compare the results. Here is how the original version works:

> (picture-of-rocket 5555)

image

And here is the second one:
> (picture-of-rocket.v2 5555)

image

No matter what number you give to picture-of-rocket.v2, if it is over 60, you get the same scene. In particular, when you run

> (animate picture-of-rocket.v2)

the rocket descends and sinks halfway into the ground before it stops.

Stop! What do you think we want to see?

Landing the rocket this far down is ugly. Then again, you know how to fix this aspect of the program. As you have seen, BSL knows an arithmetic of images. When place-image adds an image to a scene, it uses its center point as if it were the whole image, even though the image has a real height and a real width. As you may recall, you can measure the height of an image with the operation image-height. This function comes in handy here because you really want to fly the rocket only until its bottom touches the ground.

Putting one and one together you can now figure out that

(- 60 (/ (image-height ) 2))

is the point at which you want the rocket to stop its descent. You could figure this out by playing with the program directly, or you can experiment in the interactions area with your image arithmetic.

Here is a first attempt:
(place-image  50 (- 60 (image-height ))
             (empty-scene 100 60))
Now replace the third argument in the above application with

(- 60 (/ (image-height ) 2))

Stop! Conduct the experiments. Which result do you like better?

(define (picture-of-rocket.v3 height)
  (cond
    [(<= height (- 60 (/ (image-height ) 2)))
     (place-image  50 height
                  (empty-scene 100 60))]
    [(> height (- 60 (/ (image-height ) 2)))
     (place-image  50 (- 60 (/ (image-height ) 2))
                  (empty-scene 100 60))]))

Figure 6: Landing a rocket (version 3)

When you think and experiment along these lines, you eventually get to the program in figure 6. Given some number, which represents the height of the rocket, it first tests whether the rocket’s bottom is above the ground. If it is, it places the rocket into the scene as before. If it isn’t, it places the rocket’s image so that its bottom touches the ground.

One Program, Many Definitions

Now suppose your friends watch the animation but don’t like the size of your canvas. They might request a version that uses 200-by-400 scenes. This simple request forces you to replace 100 with 400 in five places in the program and 60 with 200 in two other places— not to speak of the occurrences of 50, which really means “middle of the canvas.”

Stop! Before you read on, try to do just that so that you get an idea of how difficult it is to execute this request for a five-line program. As you read on, keep in mind that programs in the world consist of 50,000 or 500,000 or even 5,000,000 or more lines of program code.

In the ideal program, a small request, such as changing the sizes of the canvas, should require an equally small change. The tool to achieve this simplicity with BSL is define. In addition to defining functions, you can also introduce constant definitions, which assign some name to a constant. The general shape of a constant definition is straightforward:

(define Name Expression)

Thus, for example, if you write down

(define HEIGHT 60)

in your program, you are saying that HEIGHT always represents the number 60. The meaning of such a definition is what you expect. Whenever DrRacket encounters HEIGHT during its calculations, it uses 60 instead.

(define (picture-of-rocket.v4 h)
  (cond
    [(<= h (- HEIGHT (/ (image-height ROCKET) 2)))
     (place-image ROCKET 50 h (empty-scene WIDTH HEIGHT))]
    [(> h (- HEIGHT (/ (image-height ROCKET) 2)))
     (place-image ROCKET
                  50 (- HEIGHT (/ (image-height ROCKET) 2))
                  (empty-scene WIDTH HEIGHT))]))
 
(define WIDTH 100)
(define HEIGHT 60)
(define ROCKET )

Figure 7: Landing a rocket (version 4)

Now take a look at the code in figure 7, which implements this simple change and also names the image of the rocket. Copy the program into DrRacket; and after clicking RUN, evaluate the following interaction:

> (animate picture-of-rocket.v4)

Confirm that the program still functions as before.

The program in figure 7 consists of four definitions: one function definition and three constant definitions. The numbers 100 and 60 occur only twice— once as the value of WIDTH and once as the value of HEIGHT. You may also have noticed that it uses h instead of height for the function parameter of picture-of-rocket.v4. Strictly speaking, this change isn’t necessary because DrRacket doesn’t confuse height with HEIGHT, but we did it to avoid confusing you.

When DrRacket evaluates (animate picture-of-rocket.v4), it replaces HEIGHT with 60, WIDTH with 100, and ROCKET with the image every time it encounters these names. To experience the joys of real programmers, change the 60 next to HEIGHT into a 400 and click RUN. You see a rocket descending and landing in a 100 by 400 scene. One small change did it all.

In modern parlance, you have just experienced your first program refactoring. Every time you reorganize your program to prepare yourself for likely future change requests, you refactor your program. Put it on your resume. It sounds good, and your future employer probably enjoys reading such buzzwords, even if it doesn’t make you a good programmer. What a good programmer would never live with, however, is having a program contain the same expression three times:

(- HEIGHT (/ (image-height ROCKET) 2))

Every time your friends and colleagues read this program, they need to understand what this expression computes, namely, the distance between the top of the canvas and the center point of a rocket resting on the ground. Every time DrRacket computes the value of the expressions, it has to perform three steps: (1) determine the height of the image; (2) divide it by 2; and (3) subtract the result from HEIGHT. And, every time, it comes up with the same number.

This observation calls for the introduction of one more definition:
(define ROCKET-CENTER-TO-TOP
  (- HEIGHT (/ (image-height ROCKET) 2)))
Now substitute ROCKET-CENTER-TO-TOP for the expression (- HEIGHT (/ (image-height ROCKET) 2)) in the rest of the program. You may be wondering whether this definition should be placed above or below the definition for HEIGHT. More generally, you should be wondering whether the ordering of definitions matters. The answer is that for constant definitions, the order matters; and for function definitions, it doesn’t. As soon as DrRacket encounters a constant definition, it determines the value of the expression and then associates the name with this value. For example,
(define HEIGHT (* 2 CENTER))
(define CENTER 100)
causes DrRacket to complain that “CENTER is used before its definition,” when it encounters the definition for HEIGHT. In contrast,
(define CENTER 100)
(define HEIGHT (* 2 CENTER))
works as expected. First, DrRacket associates CENTER with 100. Second, it evaluates (* 2 CENTER), which yields 200. Finally, DrRacket associates 200 with HEIGHT.

While the order of constant definitions matters, it does not matter where you place constant definitions relative to function definitions. Indeed, if your program consists of many function definitions, their order doesn’t matter either, though it is good to introduce all constant definitions first, followed by the definitions of functions in decreasing order of importance. When you start writing your own multi-definition programs, you will see why this ordering matters.

; constants
(define WIDTH  100)
(define HEIGHT  60)
(define MTSCN  (empty-scene WIDTH HEIGHT))
(define ROCKET )
(define ROCKET-CENTER-TO-TOP
  (- HEIGHT (/ (image-height ROCKET) 2)))
 
; functions
(define (picture-of-rocket.v5 h)
  (cond
    [(<= h ROCKET-CENTER-TO-TOP)
     (place-image ROCKET 50 h MTSCN)]
    [(> h ROCKET-CENTER-TO-TOP)
     (place-image ROCKET 50 ROCKET-CENTER-TO-TOP MTSCN)]))

Figure 8: Landing a rocket (version 5)

The program also contains two line comments, introduced with semicolons (“;”). While DrRacket ignores such comments, people who read programs should not because comments are intended for human readers. It is a “back channel” of communication between the author of the program and all of its future readers to convey information about the program.

Once you eliminate all repeated expressions, you get the program in figure 8. It consists of one function definition and five constant definitions. Beyond the placement of the rocket’s center, these constant definitions also factor out the image itself as well as the creation of the empty scene.

Before you read on, ponder the following changes to your program:

  • How would you change the program to create a 200-by-400 scene?

  • How would you change the program so that it depicts the landing of a green UFO (unidentified flying object)? Drawing the UFO is easy:

    (overlay (circle 10 "solid" "green")
             (rectangle 40 4 "solid" "green"))

  • How would you change the program so that the background is always blue?

  • How would you change the program so that the rocket lands on a flat rock bed that is 10 pixels higher than the bottom of the scene? Don’t forget to change the scenery, too.

Better than pondering is doing. It’s the only way to learn. So don’t let us stop you. Just do it.

Magic Numbers Take another look at picture-of-rocket.v5. Because we eliminated all repeated expressions, all but one number disappeared from this function definition. In the world of programming, these numbers are called magic numbers, and nobody likes them. Before you know it, you forget what role the number plays and what changes are legitimate. It is best to name such numbers in a definition.

Here we actually know that 50 is our choice for an x-coordinate for the rocket. Even though 50 doesn’t look like much of an expression, it really is a repeated expression, too. Thus, we have two reasons to eliminate 50 from the function definition, and we leave it to you to do so.

One More Definition

Recall that animate actually applies its functions to the number of clock ticks that have passed since it was first called. That is, the argument to picture-of-rocket isn’t a height but a time. Our previous definitions of picture-of-rocket use the wrong name forDanger ahead! This section introduces one piece of knowledge from physics. If physics scares you, skip it on a first reading; programming doesn’t require physics knowledge. the argument of the function; instead of h— short for height— it ought to use t for time:
(define (picture-of-rocket t)
  (cond
    [(<= t ROCKET-CENTER-TO-TOP)
     (place-image ROCKET 50 t MTSCN)]
    [(> t ROCKET-CENTER-TO-TOP)
     (place-image ROCKET
                  50 ROCKET-CENTER-TO-TOP
                  MTSCN)]))
And this small change to the definition immediately clarifies that this program uses time as if it were a distance. What a bad idea.

Even if you have never taken a physics course, you know that a time is not a distance. So somehow our program worked by accident. Don’t worry, though; it is all easy to fix. All you need to know is a bit of rocket science, which people like us call physics.

Physics?!? Well, perhaps you have already forgotten what you learned in that course. Or perhaps you have never taken a course on physics because you are way too young or gentle. No worries. This happens to the best programmers all the time because they need to help people with problems in music, economics, photography, nursing, and all kinds of other disciplines. Obviously, not even programmers know everything. So they look up what they need to know. Or they talk to the right kind of people. And if you talk to a physicist, you will find out that the distance traveled is proportional to the time:

image

That is, if the velocity of an object is v, then the object travels d miles (or meters or pixels or whatever) in t seconds.

Of course, a teacher ought to show you a proper function definition:

image

because this tells everyone immediately that the computation of d depends on t and that v is a constant. A programmer goes even further and uses meaningful names for these one-letter abbreviations:
(define V 3)
 
(define (distance t)
  (* V t))
This program fragment consists of two definitions: a function distance that computes the distance traveled by an object traveling at a constant velocity, and a constant V that describes the velocity.

You might wonder why V is 3 here. There is no special reason. We consider 3 pixels per clock tick a good velocity. You may not. Play with this number and see what happens with the animation.

; properties of the "world" and the descending rocket
(define WIDTH  100)
(define HEIGHT  60)
(define V 3)
(define X 50)
 
; graphical constants
(define MTSCN  (empty-scene WIDTH HEIGHT))
(define ROCKET )
(define ROCKET-CENTER-TO-TOP
  (- HEIGHT (/ (image-height ROCKET) 2)))
 
; functions
(define (picture-of-rocket.v6 t)
  (cond
    [(<= (distance t) ROCKET-CENTER-TO-TOP)
     (place-image ROCKET X (distance t) MTSCN)]
    [(> (distance t) ROCKET-CENTER-TO-TOP)
     (place-image ROCKET X ROCKET-CENTER-TO-TOP MTSCN)]))
 
(define (distance t)
  (* V t))

Figure 9: Landing a rocket (version 6)

Now we can fix picture-of-rocket again. Instead of comparing t with a height, the function can use (distance t) to calculate how far down the rocket is. The final program is displayed in figure 9. It consists of two function definitions: picture-of-rocket.v6 and distance. The remaining constant definitions make the function definitions readable and modifiable. As always, you can run this program with animate:

> (animate picture-of-rocket.v6)

In comparison to the previous versions of picture-of-rocket, this one shows that a program may consist of several function definitions that refer to each other. Then again, even the first version used + and /— it’s just that you think of those as built into BSL.

As you become a true-blue programmer, you will find out that programs consist of many function definitions and many constant definitions. You will also see that functions refer to each other all the time. What you really need to practice is to organize them so that you can read them easily, even months after completion. After all, an older version of you— or someone else— will want to make changes to these programs; and if you cannot understand the program’s organization, you will have a difficult time with even the smallest task. Otherwise, you mostly know what there is to know.

You Are a Programmer Now

The claim that you are a programmer may have come as a surprise to you at the end of the preceding section, but it is true. You know all the mechanics that there are to know about BSL. You know that programming uses the arithmetic of numbers, strings, images, and whatever other data your chosen programming languages support. You know that programs consist of function and constant definitions. You know, because we have told you, that in the end, it’s all about organizing these definitions properly. Last but not least, you know that DrRacket and the teachpacks support lots of other functions and that DrRacket’s HelpDesk explains what these functions do.

You might think that you still don’t know enough to write programs that react to keystrokes, mouse clicks, and so on. As it turns out, you do. In addition to the animate function, the 2htdp/universe library provides other functions that hook up your programs to the keyboard, the mouse, the clock, and other moving parts in your computer. Indeed, it even supports writing programs that connect your computer with anybody else’s computer around the world. So this isn’t really a problem.

In short, you have seen almost all the mechanics of putting together programs. If you read up on all the functions that are available, you can write programs that play interesting computer games, run simulations, or keep track of business accounts. The question is whether this really means you are a programmer. Are you?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 
Stop! Don’t turn the page yet. Think!

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Not!

When you look at the “programming” bookshelves in a random bookstore, you will see loads of books that promise to turn you into a programmer on the spot. Now that you have worked your way through some first examples, however, you probably realize that this cannot possibly happen.

Acquiring the mechanical skills of programming— learning to write expressions that the computer understands, getting to know which functions and libraries are available, and similar activities— isn’t helping you all that much with real programming. If it were, you could equally well learn a foreign language by memorizing a thousand words from the dictionary and a few rules from a grammar book.

Good programming is far more than the mechanics of acquiring a language. Most importantly, it is about keeping in mind that programmers create programs for other people to read them in the future. A good program reflects the problem statements and its important concepts. It comes with a concise self-description. Examples illustrate this description and relate it back to the problem. The examples make sure that the future reader knows why and how your code works. In short, good programming is about solving problems systematically and conveying the system within the code. Best of all, this approach to programming actually makes programming accessible to everyone— so it serves two masters at once.

The rest of this book is all about these things; very little of the book’s content is actually about the mechanics of DrRacket, BSL, or libraries. The book shows you how good programmers think about problems. And, you will even learn that this way of solving problems applies to other situations in life, such as the work of doctors, journalists, lawyers, and engineers.

Oh, and by the way, the rest of the book uses a tone that is more appropriate for a serious text than this Prologue. Enjoy!

Note on What This Book Is Not About Many introductory books on programming contain a lot of material about the authors’ favorite application discipline for programming: puzzles, mathematics, physics, music, and so on. To some extent, including such material is natural because programming is obviously useful in all these areas. Then again, this kind of material distracts from proper programming and usually fails to tease apart the incidental from the essential. Hence this book focuses on programming and problem solving and what computer science can teach you in this regard. We have made every attempt to minimize the use of knowledge from other areas; for those few occasions when we went too far, we apologize.

    ← prev  up  next →